Det här provet och dess innehåll (texter, bilder, beskrivningar och frågor) © Skolverket, Prov - och bedömningsenheten. Källa: Skolverket.se.
Version 1: Tillgång till internet i hemmet – Diagram.
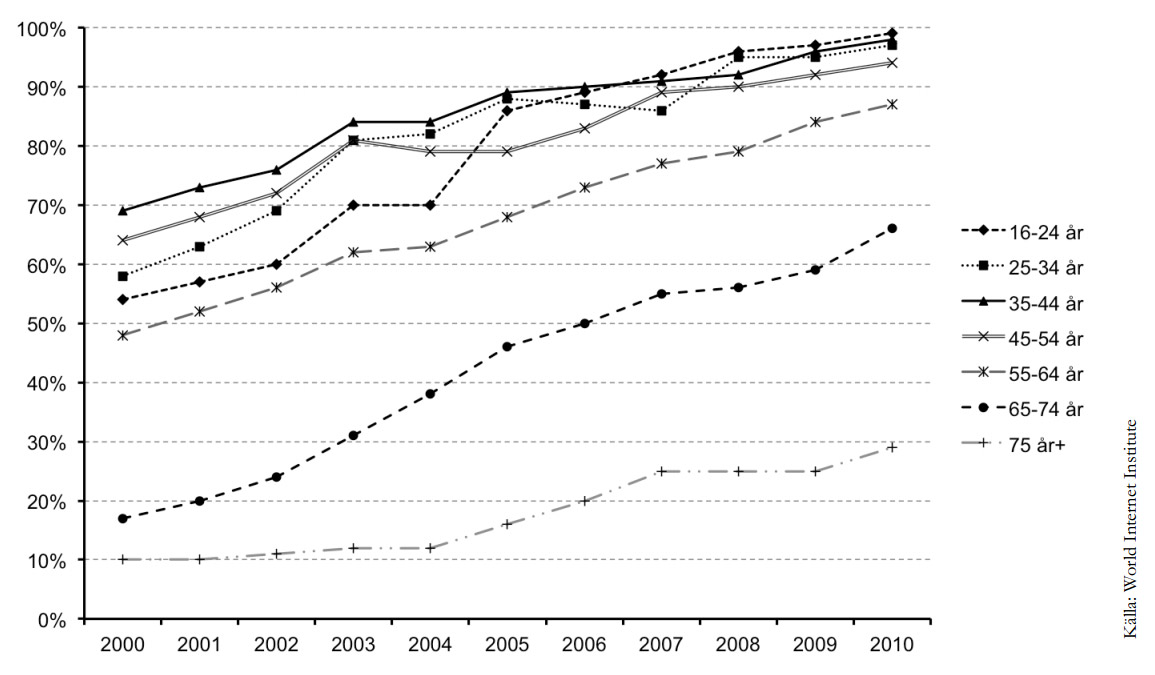
Ett urval av cirka 2 000 invånare i Sverige fick under åren 2000–2010 svara på frågor angående internet. Nedanstående diagram visar hur stor andel (%) i olika åldersgrupper som hade tillgång till internet i hemmet.
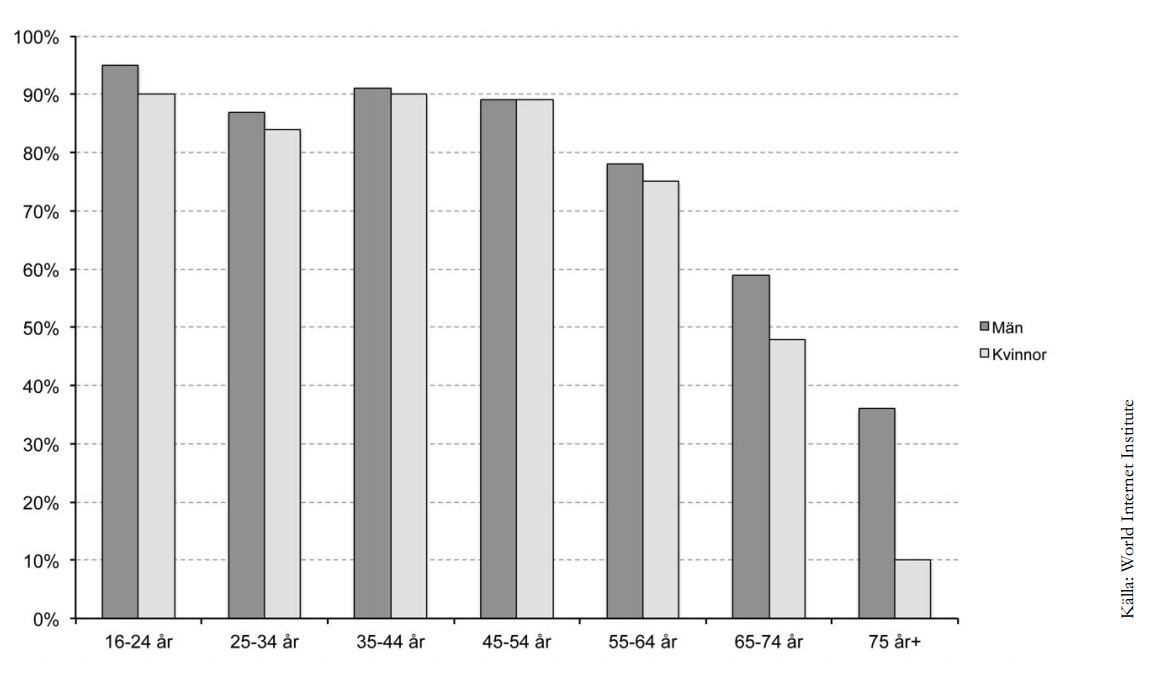
Nedanstående diagram visar hur stor andel (%) män respektive kvinnor som hade tillgång till internet i hemmet 2007.